机器学习（一）【上页】

大数据的定义：Volume（大量），Velocity（高速），Variety（多样性），Value（低价值密度）。

基础理论包括：数学，统计学，神经科学，认知科学，控制学。

弱人工智能：计算智能（存储，计算），感知智能（听，看，说，辨别），认知智能（理解，思考），目前在认知智能上发展，属于强人工智能的边界。

数据的发展趋势：

• 总量呈指数级增长。
• 数据结构会发生巨大的变化。
• 数据组织会发生巨大的变化。

数据的问题：

• 需要大量数据作为支撑。
• 可利用的数据量是小数据。

数据的三大特征：数据外部化，人工智能，价值。

决策树（Decision Tree）

从给定训练集学得一个树型模型用以对新示例分类，是基于树结构来进行决策，符合人类在面临决策性问题的一种自然处理机制。

对于决策树的关注点在于三个：

• 如何进行分裂？
• 如何选择分类属性？
• 何时停止分裂？

信息熵：给定训练集D，目标属性C={C1,C2,…,Cm}，那么我们有Ci在样本中出现的频率Pi，计算公式为：

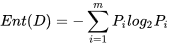
熵是反映数据的混沌程度，值越大，越混乱（所以宇宙的熵是在一直增大的，到了阈值会重置），信息熵是算法ID3的分类指标。

信息增益：属性A有v个不同值（a1,a2,…,av)，可用A将S划分为v个子集，Sj包含S中在A上具有属性值aj，计算公式为：

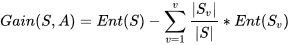
信息增益是ID3的参考指标。

信息增益率：根据信息增益和子集的信息熵得到的比率，计算公式为：

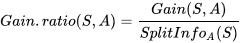
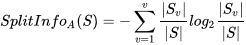
决策树的另一个改进算法是C4.5，使用了增益率做指标。

基尼系数：这是一个表达分配平等的系数，可以用于表达分布是否均匀。基尼系数越小，代表分布越均匀。在决策树的另一个算法CART中使用了该指标，计算公式为：

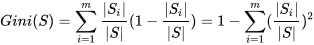
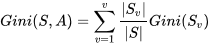
随机森林（Random Forest）

属于Bagging算法（Bootstrap Aggregating），使用CART做弱学习器。

RF的一般逻辑是：优先从特征集中随机选取少量特征，通常是特征总数的开方，依据随机选择的特征生成树型模型。在待所有树型生成完毕，每个样本都会被计算，最后的结果中，可以采用加权平均或拜占庭问题做最后的结果预测。

随机森林的特点是：

• 随机性：每棵树选取特征是随机的少量特征，通常是特征总数m的开方。
• 样本量：和一般Bagging算法不同，RF会选择和训练集样本量同样数量的样本。
• 特性：因为随机性可以降低模型方差，通常不需要做额外剪枝，可取得较好泛化能力和抗过拟合能力。

朴素贝叶斯分类（Naive Bayesian Classification)

对于给出的待分类样本，求解此样本特征的出现条件下各类别概率，哪个最大就是哪个类别。其中，朴素贝叶斯是假设各个属性条件是相互独立的。

贝叶斯定理，公式如下：

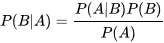
支持向量机（Support Vector Machine）

在样本空间中，训练得到位于两类训练样本正中间的划分超平面，该平面对训练样本局部扰动的容忍性最好。本质就是最优化求解，公式如下：

作业

实现SVM，随机森林，需要用实际数据验证，最后生成开发过程文档及实验结果分析文档。